快速排序的实现

1.概述

快速排序最初由一位英国计算机科学家Tony Hoare提出的。Tony Hoare是计算机科学领域的前辈之一，也是算法设计方面的专家，他在1960年代提出了快速排序算法，从那时起，快速排序就成为了许多经典排序算法之一，并且一直广泛应用在计算机科学领域。

快速排序被认为是最快的排序算法之一，因为它具有优秀的平均时间复杂度O(n logn)，此外，快速排序使用了一种高效的分治策略，可以在排序过程中大大降低内存占用，这使得它可以处理大型数据集，从而在实践中诞生出一个有效率的排序算法，因此被命名为快速排序。

2.算法

快速排序算法的主要思想是分而治之，通过将数组分成较大和较小的两个子数组，然后再递归处理两个子数组，从而达到最终有序。

快速排序算法主要有以下几个步骤：

  1. 挑选：从数组中取一个数作为基准值；可以是首尾或者中间数值，也可以是随机取一个;
  2. 分割：重新排列数组，使得比基准值小的数字都在基准值前面，比基准值大的数字都在基准值后面；
  3. 递归：将小于基准值的子数组和大于基准值的子数组按同样的方法排序；

递归的结束条件，是数组的长度小于等于1。

根据以上描述，可以写出以下递归代码：

1
2
3
4
5
6
7
void quickSort(vector<int>& nums, int left, int right) {
    if (left < right) {
        int pivotIndex = partition(nums, left, right);  // 找出基准并进行分隔，返回基准值的下标
        quickSort(nums, left, pivotIndex - 1);          // 此时left到pivotIndex - 1的值都比基准值小，对这个子数组进行排序
        quickSort(nums, pivotIndex + 1, right);         // 此时pivotIndex - 1到right的值都比基准值大，对这个子数组进行排序
    }
}

这个代码的重点在于，如何实现partition？

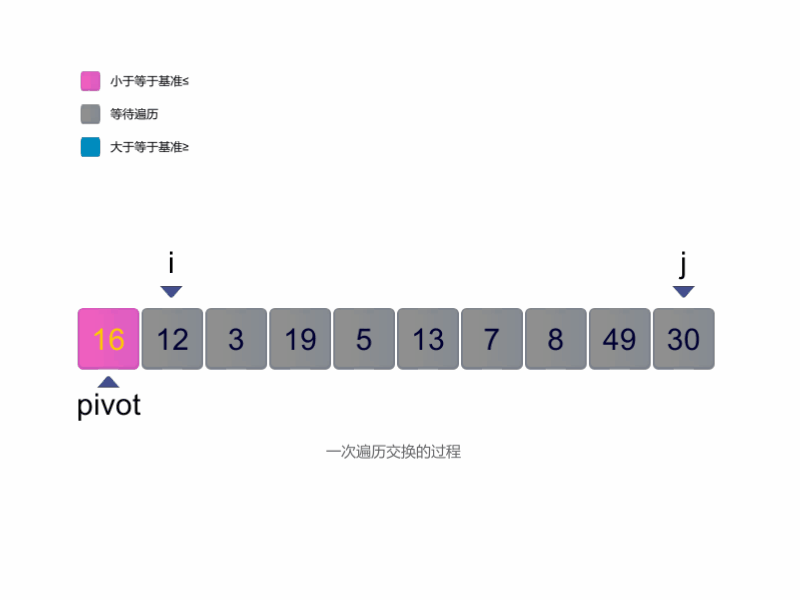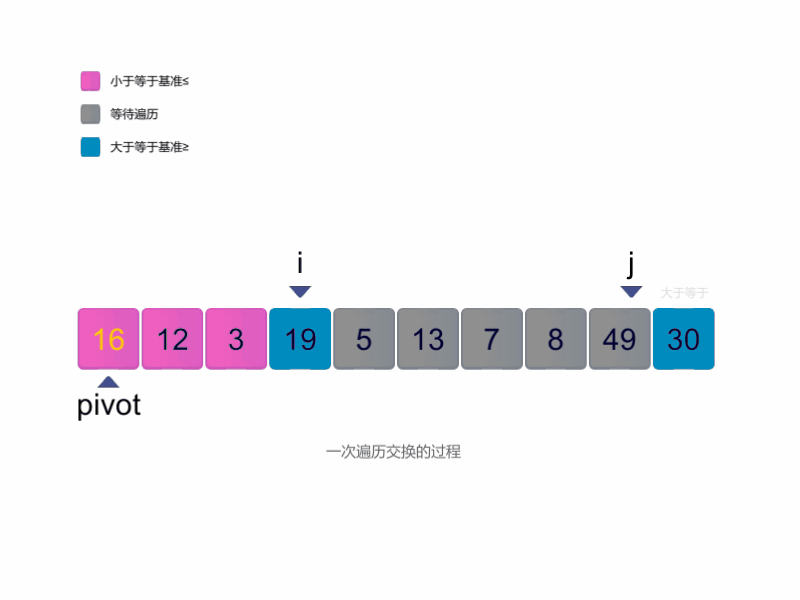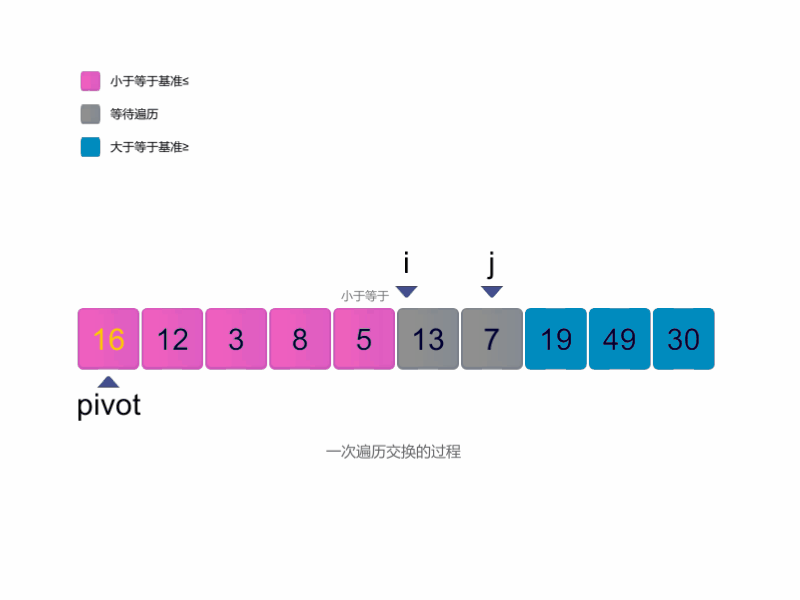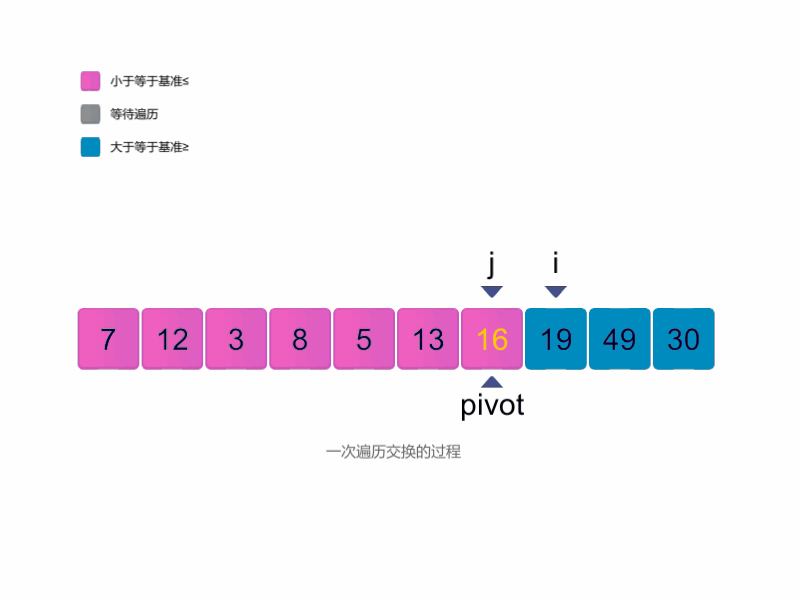
  • 首先我们选择一个基准，放在最左边；
  • 使用两个指针，一个从左往右寻找第一个大于等于基准的值， 另一个从右往左寻找第一个小于等于基准的值， 找到后交换两个值，逐渐实现目标：小于基准的在左，大于基准的在右。
  • 最终，当左边指针超过右边指针时，就可以退出循环。 此时，右边指针指向小于基准的最后一个值的下标，将其与起始位置交换，并返回这个下标。
    图1 一次partition的过程

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int partition(vector<int>& nums, int left, int right) {
    int p = left; 
    int pivot = nums[p];                        // 这里简单的将left当作基准
    int i = left + 1, j = right;                // [i, j]表示需要遍历的区间
    while (i <= j) {                            // i > j才结束，相等时也要和基准作比较
        while (i <= j && nums[i] < pivot) ++i;  // i停留在第一个大于等于基准的下标，或者找不到这样的数值，停留在j+1
        while (i <= j && nums[j] > pivot) --j;  // j停留在第一个小于等于基准的下标，或者找不到这样的数值，停留在i-1
        if (i < j) {                        // i < j时，交换i和j的值，然后i++，j--，[i, j]依旧表示需要遍历的区间
            swap(nums[i++], nums[j--]);     // 此时[left, i)都是小于等于基准的值，(j, right]都是大于等于基准的值 
        }else if (i == j){                  // i == j 只有一种情况，那就是nums[i] == pivot，此时让i+1退出循环
            i++;
        }       
    }
    swap(nums[p], nums[j]);             // 此时j == i - 1，[left, i) == [left, j]，即j是小于等于pivot的最后一个下标，将其与基准交换，
    return j;                           // j就是基准最终的位置
}

3.C++11实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
#include <iostream>
#include <vector>

using namespace std;

// 分区函数，返回分区点下标
int partition(vector<int>& nums, int left, int right) {
    int p = left; 
    int pivot = nums[p];                        // 这里简单的将left当作基准
    int i = left + 1, j = right;                // [i, j]表示需要遍历的区间
    while (i <= j) {                            // i > j才结束，相等时也要和基准作比较
        while (i <= j && nums[i] < pivot) ++i;  // i停留在第一个大于等于基准的下标，或者找不到这样的数值，停留在j+1
        while (i <= j && nums[j] > pivot) --j;  // j停留在第一个小于等于基准的下标，或者找不到这样的数值，停留在i-1
        if (i < j) {                        // i < j时，交换i和j的值，然后i++，j--，[i, j]依旧表示需要遍历的区间
            swap(nums[i++], nums[j--]);     // 此时[left, i)都是小于等于基准的值，(j, right]都是大于等于基准的值 
        }else if (i == j){                  // i == j 只有一种情况，那就是nums[i] == pivot，此时让i+1退出循环
            i++;
        }       
    }
    swap(nums[p], nums[j]);             // 此时j == i - 1，[left, i) == [left, j]，即j是小于等于pivot的最后一个下标，将其与基准交换，
    return j;                           // j就是基准最终的位置
}

// 快速排序函数
void quickSort(vector<int>& nums, int left, int right) {
    if (left < right) {
        int pivotIndex = partition(nums, left, right);
        quickSort(nums, left, pivotIndex - 1);
        quickSort(nums, pivotIndex + 1, right);
    }
}

int main() {
        // 测试用例
        vector<vector<int>> test_case = {
        {2, 2},
        {1, 2},
        {2, 1},
        {2, 2, 2, 2, 2},
        {1, 2, 3, 4, 5},
        {5, 4, 3, 2, 1},
    };

        // 加一些随机数组
        srand(time(0));
        for (int i = 0; i < 1000; i++){
                int len = rand() % 100 + 1;
                vector<int> nums(len);
                for (int j = 0; j < len; j++){
                        nums.push_back(rand() % 100);
                }
                test_case.push_back(nums);
        }

        for (auto nums : test_case){
                quickSort(nums, 0, nums.size() - 1);

                for (int i = 1; i < nums.size(); i++){
                        if (nums[i - 1] > nums[i]){
                                cout << "error" << endl;
                                return 0;
                        }
                }
        }

        cout << "all is ok" << endl;
        return 0;
}

4.时间复杂度分析

快速排序每次partition的过程，都需要遍历一次数组，复杂度为O(n)。

最好的情况下，每次分区都能分成大小相同的两个子数组，需要log2n次递归。总体复杂度为O(n logn)

而在最坏的情况下，每次分区都有一个子数组为空，即所有数据都大于或都小于基准值，此时需要n次递归。总体复杂度为O(n2)

在平均情况下，快速排序的时间复杂度也是O(n logn)，这个可以用数学归纳法来证明。具体证明过程可以参考维基百科。

5.局限

快速排序在大多数情况下都是最快的排序算法之一，但并不是完美的。

对于某些非常特殊的输入，快速排序可能会变得非常慢，因为它的时间复杂度在最坏情况下是O(n2)。

因此，有时候人们会使用其他排序算法，比如归并排序或堆排序，来替代快速排序，以确保排序的时间复杂度始终稳定在O(n logn)。

此外，还有一些特定于某些场景的排序算法，如桶排序、计数排序、基数排序等可以在特定的情况下更快，但其适用范围有限。

因此，具体取决于输入数据的特点和排序场景，选择合适的排序算法很重要。

6.优化

  1. 选择基准的时候，可以采用三数取中法：从最左、最右、和中间三个位置，取三个数中间的值作为基准，尽量使数组分割均匀；
  2. 当待排序的数组分割到一定大小的时候，使用插入排序。这是因为对于很小和部分有序的数组，快排不如插排好。
  3. 在一次分割结束后，可以把与基准相等的元素聚在一起，继续下次分割时，不用再对基准相等的元素进行分割。

参考

算法
#算法
快速排序的实现
https://blog.supersource.top/qsort/
作者
看热闹的咸鱼
发布于
2023年4月10日
许可协议