double类型中可精确表达的最大正整数

之前在项目中，使用 redis的 zset来实现排行榜，由于 zset中的分数使用了 double类型，而我们排行的数值都是整数，所以引起一个问题：

• 在 double中，能精确表示的，不会丢失精度的最大正整数是多少呢？

先说结论：是 ${2}^{53}-1$ ，即 9,007,199,254,740,991。

1. IEEE 754标准

在 IEEE 754标准中，规定了浮点数的二进制科学计数法，一个64位浮点数在内存中分为三个部分：

• 符号位(Sign): 0表示正数，1表示负数
• 指数位(Exponent): 科学计数法中的指数，采用移位存储
• 尾数部分(Mantissa): 有效数字

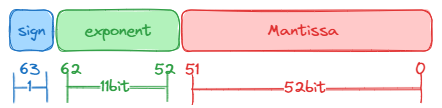
根据 IEEE754标准，一个 double类型共64位(0~63)，其中最高位(63)存储符号位，指数位共11位(52~62)，尾数部分52位(0~51)。

虽然有了 IEEE 754 标准，但是各家在实现上还是有一些区别，尤其是舍入规则上。这导致了跨平台，尤其是跨 CPU 架构的情况下，执行同一个浮点数计算得到的结果可能不一样

2. 二进制的科学计数法

十进制的科学计数法，数字可以写成 ${a}\times{10^n}$，例如 2074390000可以写成 ${2.07439}\times10^9$。

类似的，二进制也可以这样表示，例如，1101.101可以写成 ${1.101101}\times2^3$。

那么，带有小数的二进制，和十进制之间是怎么互相转换的呢？

二进制转十进制比较简单，例如，1101.101= ${1}\times{2^3} + 1\times{2^2}+0\times{2^1}+1\times{2^0} +1\times{2^{-1}}+ 0\times{2^{-2}}+ 1\times{2^{-3}}$=13.625

而十进制转二进制，要分为整数部分和小数部分，以上面的13.625为例，分为整数部分13和小数部位0.625

整数部分，通过不停地除以2直到0，取余数来得到：

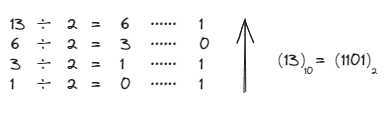
小数部分，通过不停地乘以2直到0，取整数部分来得到：

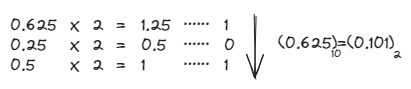
对于整数部分来说，不停地整除2，总是能到达0的，可以完整地转成二进制，但对于小数来说，不停地乘2减1，有可能永远也得不到0，这时候只能保存一定的精度了。

尾数保留精度时，并不是直接将第53位丢弃。IEEE 754 标准中定义了几种常见的舍入模式，但标准并没有具体规定编程语言或编译器必须采用哪种舍入模式作为默认行为，这也是导致不同平台或环境下的浮点数运算结果不一致的原因之一。

3. double在内存中的表示

根据 IEEE标准和二进制科学计数法，你可能觉得 double的 0.3，用二进制科学计数法写成 ${1.00110011001}\times2^{-2}$，那在内存中应该是这样的：

但实际上是下面这样：

• 首先，这个指数位的-2，和整数在内存中的表示不同，并不使用最高位作为符号位，而是使用偏移算法：存储的数据=元数据+1023，所以-2在指数位中存储的是-2+1023=1021，即01111111101，11位二进制范围是0~2047，所以指数位范围是-1022~1023（0和2047被用作特殊值处理，见下面）
• 其次，有效数字的表示，由于二进制的科学计数法总是写成${1.x}\times2^n$，第一位总是1，所以在内存中干脆不存储这一位，这样有效数字可以多表示一位。

4. 非规约形式的浮点数

除了规约浮点数，IEEE754-1985标准采用非规约浮点数，用来解决填补绝对意义下最小规格数与零的距离。
如果浮点数的指数部分的编码值是0，分数部分非零，那么这个浮点数将被称为非规约形式的浮点数。
这种情况下，尾数部分没有前导的1，即非规约浮点数的尾数小于1且大于0，此时表示的是非常接近0的小数。
除此之外，还有三种特殊值：

• 如果指数是0并且尾数的小数部分是0，这个数是±0（和符号位相关）
• 如果指数是2047(全为1)并且尾数的小数部分是0，这个数是±无穷大（同样和符号位相关）
• 如果指数是2047(全为1)并且尾数的小数部分不是0，这个数是非数字（NaN）

5. double所能表示的精确的最大正整数

我们将尾数部分全都置1，再加上隐藏的1，可以形成一个53位的二进制数：11111111111111111111111111111111111111111111111111111
再把指数部分设成52+1023，形成的数，就是 ${2}^{53}-1$ ，这就是double所能表示的精确的最大正整数。

而如果再加1，会怎样呢？尾数部分为变成0，而指数加1，变成${2}^{53}$，但这个数已经不精确了，我们用python来测试一下：

>>> a = 9007199254740991.0
>>> a - 1
9007199254740990.0
>>> a + 1
9007199254740992.0
>>> a + 2
9007199254740992.0
>>> a + 3
9007199254740994.0
>>> a - 1 == a
False
>>> a + 1 == a + 2
True

可以看到，这里无法区分出9007199254740992和9007199254740993这两个数，因为它们在内存中的表现是一样的，如下图所示，最后黑色的0和1是被丢弃的，而只保留了52位尾数之后，两个数字就变成一样的，无法精确区分这两个数字了。

参考资料

• 维基百科 IEEE 754